conditional dependence
1. Simple picture
Take two independent events \(A\) and \(B\) in the figure below, where each cell represents an equally likely outcome:
We see that \(P(B) = P(B \mid A) = \frac{1}{2}\).
Then, consider what happens when we condition on \(C\). We can think about restricting our attention to a specific region of the sample space:
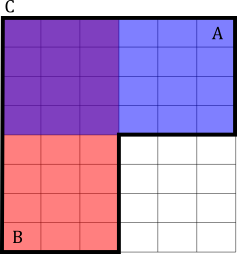
Now, \(P(B \mid C) = \frac{2}{3} \neq \frac{1}{2} = P(B \mid C,A)\).
2. Explaining Away
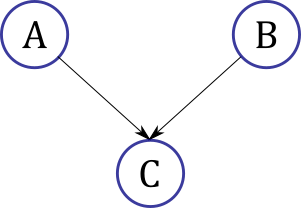
If \(A\) and \(B\) are two possible causes of \(C\), then the directed graphical model is:
Let's say that \(A\) encodes whether or not has rained, \(B\) encodes whether or not the sprinkler has gone off, and \(C\) encodes whether or not the grass is wet:
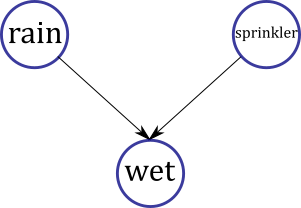
Then, conditioned on the fact that the grass is wet, \(A\) and \(B\) are not independent. That is, if we later learn that it rained, this decreases our belief that the sprinkler has gone off.
2.1. Story 1
The events of raining and sprinkling are independent. When we learn that it is wet outside, our belief that it has rained or sprinkled goes up, because wet grass can only be caused by one of those two things (in our model at least). If we additionally learn that it has rained, then our belief that it has sprinkled should go down, because a sprinkler event is no longer needed to explain the wet grass.
2.2. Story 2
What is going on can be phrased very simply in terms of conditional dependence. Let's say we have a domain of outcomes that we calculate probabilites for. At first, this domain is such that \(P(B\mid A) = P(B)\). Conditioning on a wet grass event moves our domain to a region where \(P(B\mid A,C) \neq P(B \mid C)\). What does this new region look like? Perhaps it looks something like the diagram below:
Then, conditioned on \(C\), \(A \cap B\) is actually very slim, so that \(P(B \mid C) \approx 50\%\) but \(P(B \mid C, A) \approx 10\%\)